Why Is The Entropy Change For Process 2 Larger Than That For Process 1?

Chapter 16. Thermodynamics

16.ii Entropy

Learning Objectives

By the terminate of this department, you lot will be able to:

• Define entropy
• Explain the relationship between entropy and the number of microstates
• Predict the sign of the entropy change for chemic and concrete processes

In 1824, at the historic period of 28, Nicolas Léonard Sadi Carnot (Figure i) published the results of an extensive written report regarding the efficiency of steam heat engines. In a later review of Carnot's findings, Rudolf Clausius introduced a new thermodynamic property that relates the spontaneous heat flow accompanying a process to the temperature at which the procedure takes place. This new property was expressed as the ratio of the reversible heat (q _rev) and the kelvin temperature (T). The term reversible process refers to a process that takes place at such a dull charge per unit that information technology is always at equilibrium and its direction can be changed (it can exist "reversed") by an infinitesimally small change is some condition. Notation that the idea of a reversible procedure is a formalism required to support the development of various thermodynamic concepts; no real processes are truly reversible, rather they are classified as irreversible.

Figure one. (a) Nicholas Léonard Sadi Carnot's enquiry into steam-powered machinery and (b) Rudolf Clausius's afterward written report of those findings led to groundbreaking discoveries about spontaneous heat period processes.

Similar to other thermodynamic properties, this new quantity is a state function, and then its modify depends only upon the initial and final states of a organisation. In 1865, Clausius named this property entropy (Due south) and divers its change for any procedure as the post-obit:

[latex]{\Delta}S = \frac{q_{\text{rev}}}{T}[/latex]

The entropy alter for a existent, irreversible procedure is then equal to that for the theoretical reversible process that involves the same initial and final states.

Entropy and Microstates

Following the work of Carnot and Clausius, Ludwig Boltzmann developed a molecular-scale statistical model that related the entropy of a system to the number of microstates possible for the system. A microstate (W) is a specific configuration of the locations and energies of the atoms or molecules that comprise a system like the post-obit:

[latex]S = k\;\text{ln}\;W[/latex]

Here one thousand is the Boltzmann constant and has a value of 1.38 × x⁻²³ J/Yard.

As for other land functions, the change in entropy for a procedure is the difference betwixt its final (S _f) and initial (S _i) values:

[latex]{\Delta}S = S_{\text{f}}\;-\;S_{\text{i}} = k\;\text{ln}\;W_{\text{f}}\;-\;one thousand\;\text{ln}\;W_{\text{i}} = chiliad\;\text{ln}\;\frac{W_{\text{f}}}{W_{\text{i}}}[/latex]

For processes involving an increase in the number of microstates, W _f > W _i, the entropy of the organization increases, ΔSouth > 0. Conversely, processes that reduce the number of microstates, W _f < West _i, yield a decrease in system entropy, ΔDue south < 0. This molecular-scale estimation of entropy provides a link to the probability that a procedure volition occur as illustrated in the side by side paragraphs.

Consider the general case of a arrangement comprised of North particles distributed among n boxes. The number of microstates possible for such a organization is n^N . For case, distributing four particles amid two boxes will result in 2⁴ = 16 dissimilar microstates every bit illustrated in Effigy 2. Microstates with equivalent particle arrangements (not considering individual particle identities) are grouped together and are called distributions. The probability that a system will exist with its components in a given distribution is proportional to the number of microstates within the distribution. Since entropy increases logarithmically with the number of microstates, the most probable distribution is therefore the one of greatest entropy.

Figure 2. The sixteen microstates associated with placing four particles in two boxes are shown. The microstates are collected into five distributions—(a), (b), (c), (d), and (e)—based on the numbers of particles in each box.

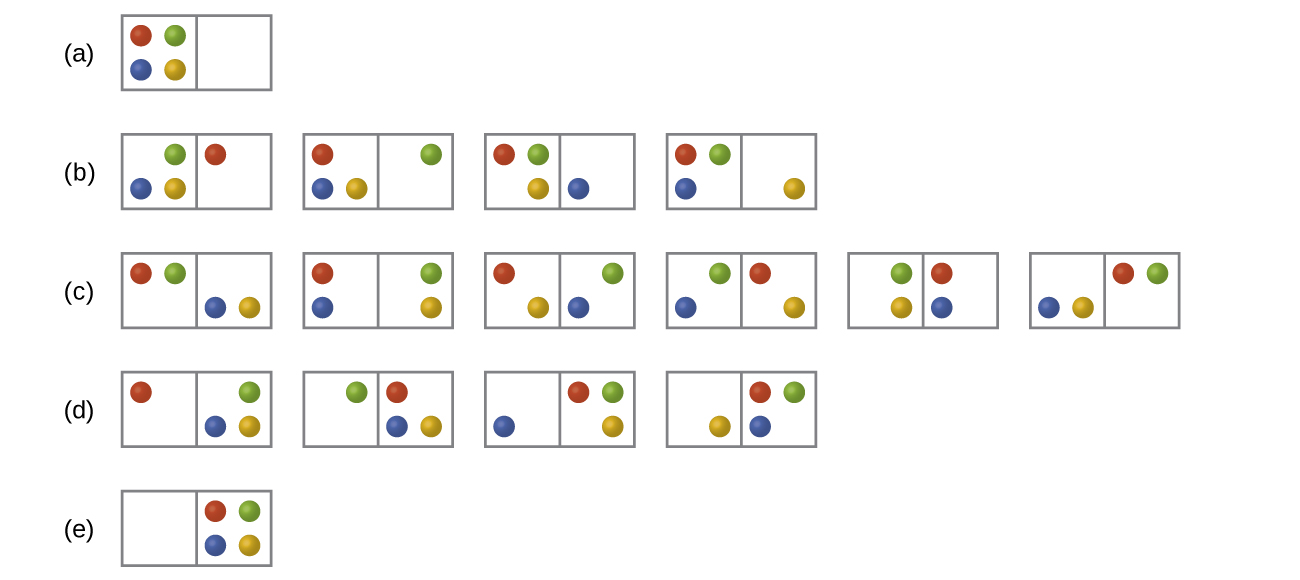
For this organisation, the nearly likely configuration is 1 of the half dozen microstates associated with distribution (c) where the particles are evenly distributed between the boxes, that is, a configuration of two particles in each box. The probability of finding the system in this configuration is or [latex]\frac{6}{xvi}[/latex] or [latex]\frac{3}{viii}[/latex]. The least probable configuration of the system is one in which all iv particles are in i box, respective to distributions (a) and (d), each with a probability of [latex]\frac{1}{16}[/latex]. The probability of finding all particles in only one box (either the left box or correct box) is and so [latex](\frac{ane}{sixteen}\;+\;\frac{1}{16}) = \frac{2}{16}[/latex] or [latex]\frac{ane}{8}[/latex].

As you add more particles to the system, the number of possible microstates increases exponentially (2 ^N ). A macroscopic (laboratory-sized) system would typically consist of moles of particles (North ~ 10²³), and the corresponding number of microstates would exist staggeringly huge. Regardless of the number of particles in the arrangement, however, the distributions in which roughly equal numbers of particles are constitute in each box are always the virtually probable configurations.

The previous clarification of an ideal gas expanding into a vacuum (Affiliate xvi.1 Spontaneity) is a macroscopic case of this particle-in-a-box model. For this organization, the near likely distribution is confirmed to be the i in which the matter is about uniformly dispersed or distributed between the ii flasks. The spontaneous process whereby the gas contained initially in one flask expands to make full both flasks equally therefore yields an increase in entropy for the system.

A similar arroyo may be used to depict the spontaneous flow of heat. Consider a organization consisting of two objects, each containing ii particles, and two units of energy (represented every bit "*") in Figure 3. The hot object is comprised of particles A and B and initially contains both energy units. The cold object is comprised of particles C and D, which initially has no energy units. Distribution (a) shows the iii microstates possible for the initial state of the system, with both units of energy contained within the hot object. If one of the two energy units is transferred, the result is distribution (b) consisting of 4 microstates. If both energy units are transferred, the consequence is distribution (c) consisting of three microstates. So, we may describe this organisation past a total of ten microstates. The probability that the heat does not period when the ii objects are brought into contact, that is, that the arrangement remains in distribution (a), is [latex]\frac{three}{10}[/latex]. More likely is the flow of oestrus to yield ane of the other ii distribution, the combined probability being [latex]\frac{seven}{x}[/latex]. The nearly probable effect is the flow of heat to yield the uniform dispersal of energy represented by distribution (b), the probability of this configuration being [latex]\frac{4}{x}[/latex]. Every bit for the previous example of affair dispersal, extrapolating this treatment to macroscopic collections of particles dramatically increases the probability of the uniform distribution relative to the other distributions. This supports the mutual observation that placing hot and cold objects in contact results in spontaneous heat flow that ultimately equalizes the objects' temperatures. And, again, this spontaneous process is as well characterized by an increase in system entropy.

Figure iii. This shows a microstate model describing the flow of estrus from a hot object to a cold object. (a) Before the heat flow occurs, the object comprised of particles A and B contains both units of energy and as represented by a distribution of three microstates. (b) If the rut flow results in an even dispersal of energy (one free energy unit transferred), a distribution of four microstates results. (c) If both energy units are transferred, the resulting distribution has 3 microstates.

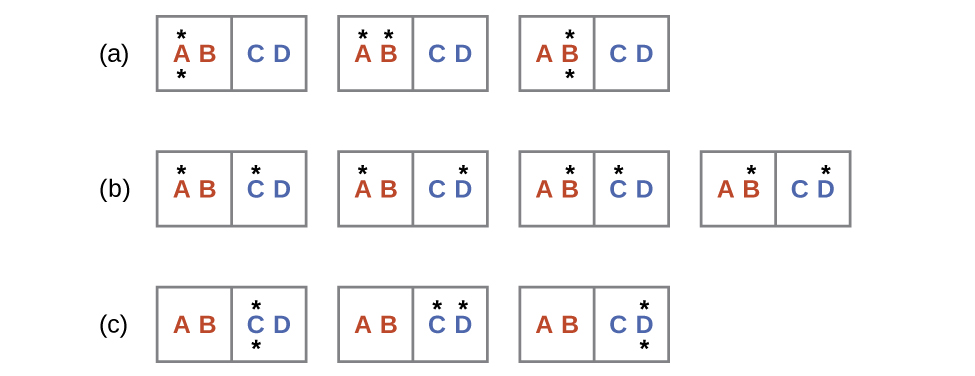
Case 1

Conclusion of ΔSouth
Consider the arrangement shown hither. What is the change in entropy for a process that converts the system from distribution (a) to (c)?

Solution
We are interested in the post-obit change:

The initial number of microstates is 1, the terminal vi:

[latex]{\Delta}S = k\;\text{ln}\;\frac{W_{\text{c}}}{W_{\text{a}}} = 1.38\;\times\;10^{-23}\;\text{J}/\text{G}\;\times\;\text{ln}\;\frac{half dozen}{1} = 2.47\;\times\;10^{-23}\;\text{J}/\text{K}[/latex]

The sign of this result is consistent with expectation; since there are more than microstates possible for the final country than for the initial state, the change in entropy should be positive.

Check Your Learning
Consider the arrangement shown in Figure 3. What is the change in entropy for the process where all the free energy is transferred from the hot object (AB) to the cold object (CD)?

Predicting the Sign of ΔS

The relationships between entropy, microstates, and thing/energy dispersal described previously allow us to make generalizations regarding the relative entropies of substances and to predict the sign of entropy changes for chemical and physical processes. Consider the phase changes illustrated in Figure 4. In the solid phase, the atoms or molecules are restricted to nearly fixed positions with respect to each other and are capable of only pocket-size oscillations about these positions. With essentially stock-still locations for the organization's component particles, the number of microstates is relatively small. In the liquid stage, the atoms or molecules are free to move over and around each other, though they remain in relatively close proximity to i some other. This increased liberty of motion results in a greater variation in possible particle locations, so the number of microstates is correspondingly greater than for the solid. As a result, South _liquid > S _solid and the process of converting a substance from solid to liquid (melting) is characterized by an increase in entropy, ΔS > 0. By the same logic, the reciprocal process (freezing) exhibits a subtract in entropy, ΔDue south < 0.

Figure 4. The entropy of a substance increases (ΔS > 0) as information technology transforms from a relatively ordered solid, to a less-ordered liquid, and so to a still less-ordered gas. The entropy decreases (ΔS < 0) as the substance transforms from a gas to a liquid and then to a solid.

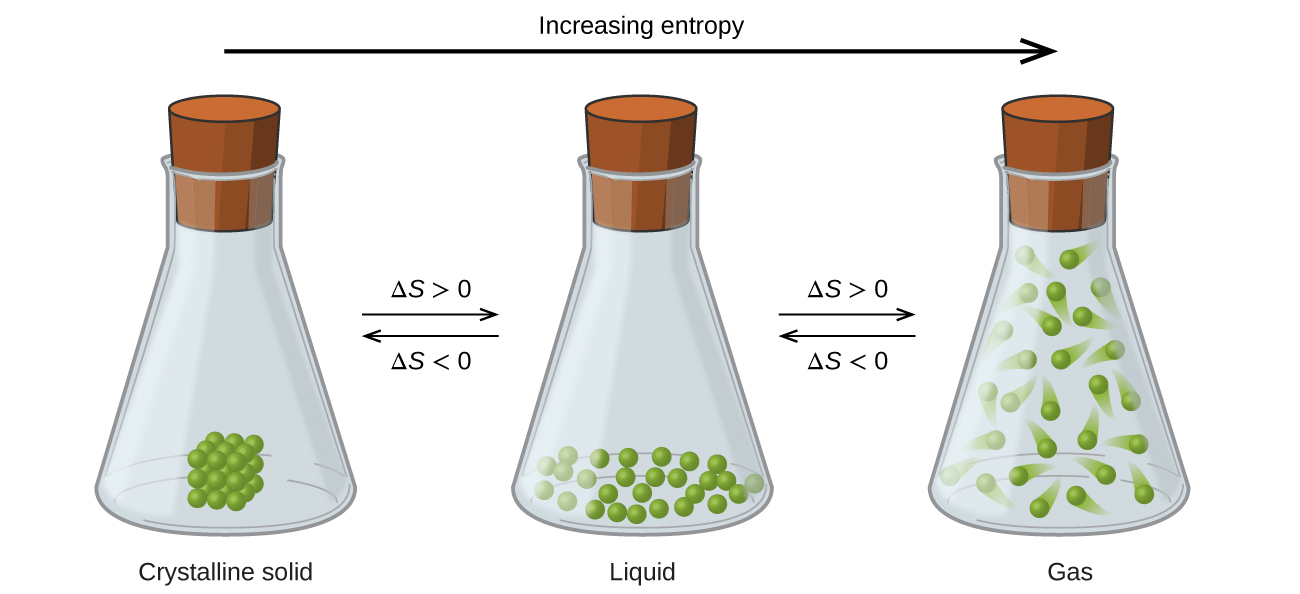
Now consider the vapor or gas phase. The atoms or molecules occupy a much greater volume than in the liquid stage; therefore each cantlet or molecule can be found in many more locations than in the liquid (or solid) stage. Consequently, for any substance, S _gas > South _liquid > Southward _solid, and the processes of vaporization and sublimation likewise involve increases in entropy, ΔS > 0. Besides, the reciprocal phase transitions, condensation and deposition, involve decreases in entropy, ΔS < 0.

Co-ordinate to kinetic-molecular theory, the temperature of a substance is proportional to the boilerplate kinetic energy of its particles. Raising the temperature of a substance will issue in more than extensive vibrations of the particles in solids and more than rapid translations of the particles in liquids and gases. At college temperatures, the distribution of kinetic energies among the atoms or molecules of the substance is also broader (more dispersed) than at lower temperatures. Thus, the entropy for any substance increases with temperature (Effigy 5).

Effigy 5. Entropy increases every bit the temperature of a substance is raised, which corresponds to the greater spread of kinetic energies. When a substance melts or vaporizes, it experiences a meaning increment in entropy.

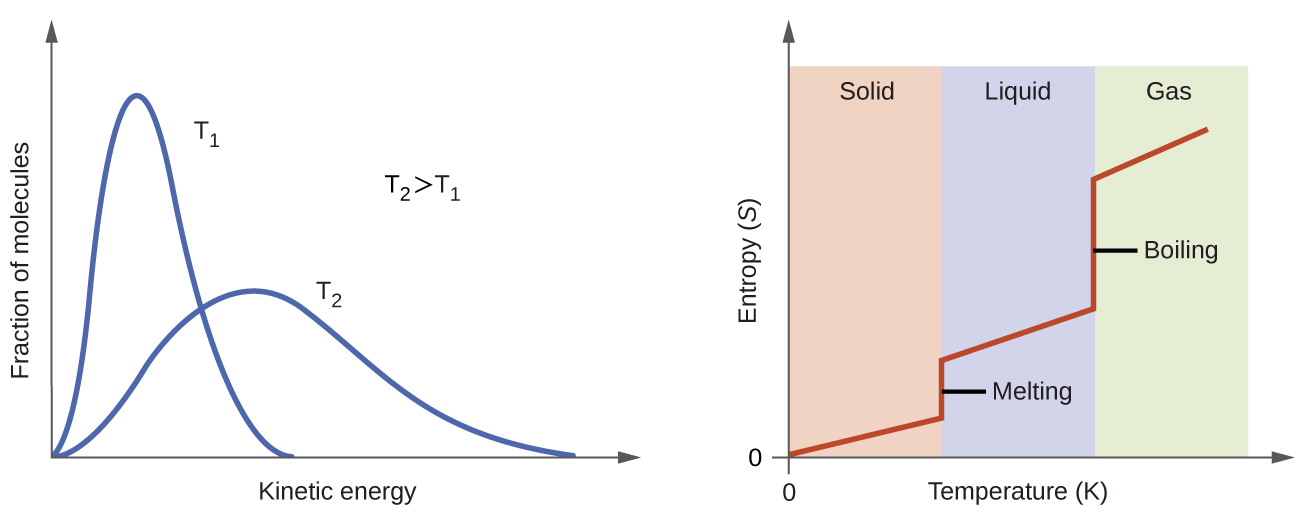
Try this simulator with interactive visualization of the dependence of particle location and freedom of motion on physical state and temperature.

The entropy of a substance is influenced by structure of the particles (atoms or molecules) that comprise the substance. With regard to atomic substances, heavier atoms possess greater entropy at a given temperature than lighter atoms, which is a consequence of the relation between a particle's mass and the spacing of quantized translational energy levels (which is a topic across the scope of our handling). For molecules, greater numbers of atoms (regardless of their masses) increase the ways in which the molecules tin can vibrate and thus the number of possible microstates and the system entropy.

Finally, variations in the types of particles affects the entropy of a arrangement. Compared to a pure substance, in which all particles are identical, the entropy of a mixture of two or more different particle types is greater. This is because of the additional orientations and interactions that are possible in a system comprised of nonidentical components. For example, when a solid dissolves in a liquid, the particles of the solid experience both a greater freedom of motion and additional interactions with the solvent particles. This corresponds to a more compatible dispersal of matter and energy and a greater number of microstates. The process of dissolution therefore involves an increment in entropy, ΔS > 0.

Considering the various factors that touch entropy allows usa to brand informed predictions of the sign of ΔS for various chemical and physical processes as illustrated in Example 2.

Example 2

Predicting the Sign of ∆S
Predict the sign of the entropy change for the post-obit processes. Indicate the reason for each of your predictions.

(a) I mole liquid water at room temperature ⟶⟶ one mole liquid h2o at 50 °C

(b) [latex]\text{Ag}^{+}(aq)\;+\;\text{Cl}^{-}(aq)\;{\longrightarrow}\;\text{AgCl}(s)[/latex]

(c) [latex]\text{C}_6\text{H}_6(fifty)\;+\;\frac{xv}{two}\text{O}_2(g)\;{\longrightarrow}\;6\text{CO}_2(g)\;+\;three\text{H}_2\text{O}(l)[/latex]

(d) [latex]\text{NH}_3(s)\;{\longrightarrow}\;\text{NH}_3(fifty)[/latex]

Solution
(a) positive, temperature increases

(b) negative, reduction in the number of ions (particles) in solution, decreased dispersal of matter

(c) negative, cyberspace decrease in the amount of gaseous species

(d) positive, phase transition from solid to liquid, net increment in dispersal of thing

Check Your Learning
Predict the sign of the enthalpy alter for the following processes. Give a reason for your prediction.

(a) [latex]\text{NaNO}_3(due south)\;{\longrightarrow}\;\text{Na}^{+}(aq)\;+\;\text{NO}_3^{\;\;-}(aq)[/latex]

(b) the freezing of liquid water

(c) [latex]\text{CO}_2(s)\;{\longrightarrow}\;\text{CO}_2(g)[/latex]

(d) [latex]\text{CaCO}(s)\;{\longrightarrow}\;\text{CaO}(s)\;+\;\text{CO}_2(m)[/latex]

Answer:

(a) Positive; The solid dissolves to give an increase of mobile ions in solution. (b) Negative; The liquid becomes a more ordered solid. (c) Positive; The relatively ordered solid becomes a gas. (d) Positive; There is a cyberspace production of one mole of gas.

Cardinal Concepts and Summary

Entropy (S) is a country function that tin be related to the number of microstates for a system (the number of means the system tin be arranged) and to the ratio of reversible estrus to kelvin temperature. Information technology may exist interpreted every bit a measure of the dispersal or distribution of affair and/or energy in a system, and information technology is often described as representing the "disorder" of the system.

For a given substance, Due south _solid < Due south _liquid < S _gas in a given physical state at a given temperature, entropy is typically greater for heavier atoms or more complex molecules. Entropy increases when a system is heated and when solutions form. Using these guidelines, the sign of entropy changes for some chemical reactions may be reliably predicted.

Key Equations

• [latex]{\Delta}S = \frac{q_{\text{rev}}}{T}[/latex]
• [latex]S = one thousand\;\text{ln}\;W[/latex]
• [latex]{\Delta}Due south = k\;\text{ln}\;\frac{W_{\text{f}}}{W_{\text{i}}}[/latex]

Chemistry End of Chapter Exercises

1. In Effigy ii all possible distributions and microstates are shown for four different particles shared betwixt two boxes. Determine the entropy change, ΔSouth, if the particles are initially evenly distributed between the two boxes, just upon redistribution all end upward in Box (b).
2. In Figure 2 all of the possible distributions and microstates are shown for four different particles shared between two boxes. Determine the entropy change, ΔSouthward, for the system when it is converted from distribution (b) to distribution (d).
3. How does the process described in the previous item relate to the system shown in Chapter 16.one Spontaneity?
4. Consider a system similar to the one in Figure ii, except that it contains half-dozen particles instead of four. What is the probability of having all the particles in just one of the 2 boxes in the case? Compare this with the like probability for the organisation of four particles that we have derived to exist equal to [latex]\frac{i}{8}[/latex]. What does this comparison tell united states of america almost even larger systems?
5. Consider the system shown in Figure 3. What is the change in entropy for the process where the energy is initially associated only with particle A, merely in the last country the energy is distributed between two different particles?
6. Consider the system shown in Figure iii. What is the modify in entropy for the process where the energy is initially associated with particles A and B, and the free energy is distributed between two particles in dissimilar boxes (one in A-B, the other in C-D)?
7. Adjust the following sets of systems in order of increasing entropy. Assume i mole of each substance and the same temperature for each member of a gear up.

   (a) H₂(k), HBrO₄(g), HBr(g)

   (b) H₂O(fifty), H₂O(g), H₂O(s)

   (c) He(g), Cl_two(k), P₄(g)

8. At room temperature, the entropy of the halogens increases from I₂ to Br₂ to Cl_ii. Explicate.
9. Consider 2 processes: sublimation of I₂(s) and melting of I₂(southward) (Annotation: the latter procedure can occur at the same temperature just somewhat higher pressure).

   [latex]\text{I}_2(s)\;{\longrightarrow}\;\text{I}_2(g)[/latex]

   [latex]\text{I}_2(s)\;{\longrightarrow}\;\text{I}_2(l)[/latex]

   Is ΔS positive or negative in these processes? In which of the processes will the magnitude of the entropy change be greater?

10. Indicate which substance in the given pairs has the higher entropy value. Explain your choices.

    (a) C₂H₅OH(l) or C₃H₇OH(l)

    (b) C₂H₅OH(fifty) or C₂H₅OH(chiliad)

    (c) 2H(thou) or H(thou)

11. Predict the sign of the entropy change for the following processes.

    (a) An ice cube is warmed to near its melting point.

    (b) Exhaled jiff forms fog on a cold forenoon.

    (c) Snow melts.

12. Predict the sign of the entropy alter for the post-obit processes. Give a reason for your prediction.

    (a) [latex]\text{Atomic number 82}^{2+}(aq)\;+\;\text{Due south}^{ii-}(aq)\;{\longrightarrow}\;\text{PbS}(s)[/latex]

    (b) [latex]2\text{Fe}(south)\;+\;3\text{O}_2(yard)\;{\longrightarrow}\;\text{Atomic number 26}_2\text{O}_3(s)[/latex]

    (c) [latex]2\text{C}_6\text{H}_{14}(fifty)\;+\;xix\text{O}_2(g)\;{\longrightarrow}\;14\text{H}_2\text{O}(chiliad)\;+\;12\text{CO}_2(g)[/latex]

13. Write the balanced chemical equation for the combustion of marsh gas, CH₄(g), to give carbon dioxide and h2o vapor. Explicate why it is difficult to predict whether ΔDue south is positive or negative for this chemical reaction.
14. Write the balanced chemic equation for the combustion of benzene, C_viH_six(l), to give carbon dioxide and h2o vapor. Would y'all look ΔS to exist positive or negative in this procedure?

Glossary

entropy (Due south)

country function that is a measure of the matter and/or energy dispersal within a organisation, adamant by the number of arrangement microstates often described as a measure out of the disorder of the organisation

microstate (West)

possible configuration or arrangement of affair and energy within a system

reversible process

procedure that takes place so slowly as to be capable of reversing direction in response to an infinitesimally pocket-sized change in weather condition; hypothetical construct that can only be approximated by real processes removed

Solutions

Answers to Chemistry End of Chapter Exercises

2. There are four initial microstates and four final microstates.
[latex]{\Delta}S = k\;\text{ln}\;\frac{W_{\text{f}}}{W_{\text{i}}} = 1.38\;\times\;10^{-23}\;\text{J}/\text{K}\;\times\;\text{ln}\;\frac{four}{4} = 0[/latex]

iv. The probability for all the particles to be on one side is [latex]\frac{1}{32}[/latex]. This probability is noticeably lower than the [latex]\frac{1}{eight}[/latex] event for the four-particle arrangement. The determination nosotros can brand is that the probability for all the particles to stay in merely ane part of the system will decrease quickly as the number of particles increases, and, for case, the probability for all molecules of gas to gather in only ane side of a room at room temperature and pressure level is negligible since the number of gas molecules in the room is very large.

half-dozen. There is but one initial country. For the last state, the free energy tin be independent in pairs A-C, A-D, B-C, or B-D. Thus, there are four final possible states.
[latex]{\Delta}S = k\;\text{ln}\;(\frac{W_{\text{f}}}{W_{\text{i}}}) = i.38\;\times\;10^{-23}\;\text{J}/\text{K}\;\times\;\text{ln}\;(\frac{4}{1}) = ane.91\;\times\;10^{-23}\;\text{J}/\text{M}[/latex]

eight. The masses of these molecules would advise the opposite trend in their entropies. The observed trend is a upshot of the more meaning variation of entropy with a physical state. At room temperature, I_two is a solid, Br₂ is a liquid, and Cl₂ is a gas.

10. (a) C₃H₇OH(l) as it is a larger molecule (more complex and more massive), and then more microstates describing its motions are bachelor at whatsoever given temperature. (b) C₂H_vOH(g) as it is in the gaseous land. (c) 2H(g), since entropy is an extensive holding, and and then two H atoms (or two moles of H atoms) possess twice equally much entropy as one cantlet (or one mole of atoms).

12. (a) Negative. The relatively ordered solid precipitating decreases the number of mobile ions in solution. (b) Negative. There is a net loss of iii moles of gas from reactants to products. (c) Positive. In that location is a net increase of seven moles of gas from reactants to products.

14. [latex]\text{C}_6\text{H}_6(l)\;+\;7.5\text{O}_2(k)\;{\longrightarrow}\;three\text{H}_2\text{O}(g)\;+\;half-dozen\text{CO}_2(thousand)[/latex]
There are 7.5 moles of gas initially, and iii + half dozen = ix moles of gas in the stop. Therefore, information technology is likely that the entropy increases as a result of this reaction, and ΔS is positive.

Source: https://opentextbc.ca/chemistry/chapter/16-2-entropy/

Posted by: toddurnow1939.blogspot.com

Share this post